Плоскость. Плоскость задается тремя произвольными точками, не принадлежащими одной прямой. Способы задания плоскости на эпюре Чем нельзя задать плоскость в пространстве

12.02.2024

В планиметрии плоскость является одной из основных фигур, поэтому, очень важно иметь ясное представление о ней. Эта статья создана с целью раскрытия этой темы. Сначала дано понятие плоскости, ее графическое представление и показаны обозначения плоскостей. Далее плоскость рассматривается вместе с точкой, прямой или другой плоскостью, при этом возникают варианты из взаимного расположения в пространстве. Во втором и третьем и четвертом пункте статьи как раз разобраны все варианты взаимного расположения двух плоскостей, прямой и плоскости, а также точки и плоскости, приведены основные аксиомы и графические иллюстрации. В заключении даны основные способы задания плоскости в пространстве.

Навигация по странице.

Плоскость – основные понятия, обозначения и изображение.

Простейшими и основными геометрическими фигурами в трехмерном пространстве являются точка, прямая и плоскость. Мы уже имеем представление о точке и прямой на плоскости . Если поместить плоскость, на которой изображены точки и прямые, в трехмерное пространство, то мы получим точки и прямые в пространстве. Представление о плоскости в пространстве позволяет получить, к примеру, поверхность стола или стены. Однако, стол или стена имеют конечные размеры, а плоскость простирается за их границы в бесконечность.

Точки и прямые в пространстве обозначаются также как и на плоскости – большими и маленькими латинскими буквами соответственно. Например, точки А и Q , прямые а и d . Если заданы две точки, лежащие на прямой, то прямую можно обозначить двумя буквами, соответствующими этим точкам. К примеру, прямая АВ или ВА проходит через точки А и В . Плоскости принято обозначать маленькими греческими буквами, например, плоскости , или .

При решении задач возникает необходимость изображать плоскости на чертеже. Плоскость обычно изображают в виде параллелограмма или произвольной простой замкнутой области.

Плоскость обычно рассматривается вместе с точками, прямыми или другими плоскостями, при этом возникают различные варианты их взаимного расположения. Переходим к их описанию.

Взаимное расположение плоскости и точки.

Начнем с аксиомы: в каждой плоскости имеются точки. Из нее следует первый вариант взаимного расположения плоскости и точки – точка может принадлежать плоскости. Другими словами, плоскость может проходить через точку. Для обозначения принадлежности какой-либо точки какой-либо плоскости используют символ «». Например, если плоскость проходит через точку А , то можно кратко записать .

Следует понимать, что на заданной плоскости в пространстве имеется бесконечно много точек.

Следующая аксиома показывает, сколько точек в пространстве необходимо отметить, чтобы они определяли конкретную плоскость: через три точки, не лежащие на одной прямой, проходит плоскость, причем только одна. Если известны три точки, лежащие в плоскости, то плоскость можно обозначить тремя буквами, соответствующими этим точкам. Например, если плоскость проходит через точки А , В и С , то ее можно обозначить АВС .

Сформулируем еще одну аксиому, которая дает второй вариант взаимного расположения плоскости и точки: имеются по крайней мере четыре точки, не лежащие в одной плоскости. Итак, точка пространства может не принадлежать плоскости. Действительно, в силу предыдущей аксиомы через три точки пространства проходит плоскость, а четвертая точка может как лежать на этой плоскости, так и не лежать. При краткой записи используют символ «», который равносилен фразе «не принадлежит».

К примеру, если точка А не лежит в плоскости , то используют краткую запись .

Прямая и плоскость в пространстве.

Во-первых, прямая может лежать в плоскости. В этом случае, в плоскости лежат хотя бы две точки этой прямой. Это устанавливается аксиомой: если две точки прямой лежат в плоскости, то все точки этой прямой лежат в плоскости. Для краткой записи принадлежности некоторой прямой данной плоскости пользуются символом «». Например, запись означает, что прямая а лежит в плоскости .

Во-вторых, прямая может пересекать плоскость. При этом прямая и плоскость имеют одну единственную общую точку, которую называют точкой пересечения прямой и плоскости. При краткой записи пересечение обозначаю символом «». К примеру, запись означает, что прямая а пересекает плоскость в точке М . При пересечении плоскости некоторой прямой возникает понятие угла между прямой и плоскостью .

Отдельно стоит остановиться на прямой, которая пересекает плоскость и перпендикулярна любой прямой, лежащей в этой плоскости. Такую прямую называют перпендикулярной к плоскости. Для краткой записи перпендикулярности используют симовл «». Для более глубокого изучения материала можете обратиться к статье перпендикулярность прямой и плоскости .

Особую значимость при решении задач, связанных с плоскостью, имеет так называемый нормальный вектор плоскости . Нормальным вектором плоскости является любой ненулевой вектор, лежащий на прямой, перпендикулярной этой плоскости.

В-третьих, прямая может быть параллельна плоскости, то есть, не иметь в ней общих точек. При краткой записи параллельности используют символ «». Например, если прямая а параллельна плоскости , то можно записать . Рекомендуем подробнее изучить этот случай, обратившись к статье параллельность прямой и плоскости .

Следует сказать, что прямая, лежащая в плоскости, делит эту плоскость на две полуплоскости. Прямая в этом случае называется границей полуплоскостей. Любые две точки одной полуплоскости лежат по одну сторону от прямой, а две точки разных полуплоскостей лежат по разные стороны от граничной прямой.

Взаимное расположение плоскостей.

Две плоскости в пространстве могут совпадать. В этом случае они имеют, по крайней мере, три общие точки.

Две плоскости в пространстве могут пересекаться. Пересечением двух плоскостей является прямая линия, что устанавливается аксиомой: если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей.

В этом случае возникает понятие угла между пересекающимися плоскостями . Отдельный интерес представляет случай, когда угол между плоскостями равен девяноста градусам. Такие плоскости называют перпендикулярными. О них мы поговорили в статье перпендикулярность плоскостей .

Наконец, две плоскости в пространстве могут быть параллельными, то есть, не иметь общих точек. Рекомендуем ознакомиться со статьей параллельность плоскостей , чтобы получить полное представление об этом варианте взаимного расположения плоскостей.

Способы задания плоскости.

Сейчас мы перечислим основные способы задания конкретной плоскости в пространстве.

Во-первых, плоскость можно задать, зафиксировав три не лежащие на одной прямой точки пространства. Этот способ основан на аксиоме: через любые три точки, не лежащие на одной прямой, проходит единственная плоскость.

Если в трехмерном пространстве зафиксирована и задана плоскость с помощью указания координат трех ее различных точек, не лежащих на одной прямой, то мы можем написать уравнение плоскости, проходящей через три заданные точки .

Два следующих способа задания плоскости являются следствием из предыдущего. Они основаны на следствиях из аксиомы о плоскости, проходящей через три точки:

через прямую и не лежащую на ней точку проходит плоскость, притом только одна (смотрите также статью уравнение плоскости, проходящей через прямую и точку);
через две пересекающиеся прямые проходит единственная плоскость (рекомендуем ознакомиться с материалом статьи уравнение плоскости, проходящей через две пересекающиеся прямые).

Четвертый способ задания плоскости в пространстве основан на определении параллельных прямых . Напомним, что две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются. Таким образом, указав две параллельные прямые в пространстве, мы определим единственную плоскость, в которой эти прямые лежат.

Если в трехмерном пространстве относительно прямоугольной системы координат задана плоскость указанным способом, то мы можем составить уравнение плоскости, проходящей через две параллельные прямые .

В курсе средней школы на уроках геометрии доказывается следующая теорема: через фиксированную точку пространства проходит единственная плоскость, перпендикулярная к данной прямой. Таким образом, мы можем задать плоскость, если укажем точку, через которую она проходит, и прямую, перпендикулярную к ней.

Если в трехмерном пространстве зафиксирована прямоугольная система координат и задана плоскость указанным способом, то можно составить уравнение плоскости, проходящей через заданную точку перпендикулярно к заданной прямой .

Вместо прямой, перпендикулярной к плоскости, можно указать один из нормальных векторов этой плоскости. В этом случае есть возможность написать

Всякая геометрическая фигура, погруженная в пространство, состоит из некоторого множества точек пространства. Плоскость как одна из геометрических фигур, представляет собой совокупность множества точек. Из этого определения плоскости можно установить способы задания ее положения в пространстве. Для этого достаточно вспомнить аксиому сочетания – через три точки, не лежащие на одной прямой, можно провести плоскость и притом только одну.

На рис. 21 представлены способы задания положения плоскости в пространстве:

а – тремя точками, не лежащими на одной прямой;

б – прямой и точкой, взятой вне прямой;

в – двумя пересекающимися прямыми;

г – двумя параллельными прямыми.

На комплексном чертеже (рис. 22) плоскость может быть задана:

а – проекциями трех точек, не лежащих на одной прямой;

б – проекциями прямой и точки, взятой вне прямой;

в – проекциями двух пересекающихся прямых;

г – проекциями двух параллельных прямых.

Каждый из представленных на рис. 22 способов задания плоскости на чертеже может быть преобразован из одного в другой. Так, например, проведя через точки А и В (рис. 22, а) прямую, получают задание плоскости, представленное на рис. 22, б. От него можно перейти к способу, представленному на рис. 22, г, если через точку С провести прямую, параллельную прямой АВ. Если точки А, В и С соединить попарно прямыми, то получают треугольник АВС – плоскую фигуру (рис. 23), проекциями которой может быть задана плоскость на чертеже.

При этом всегда следует помнить о том, что плоскость, как геометрическая фигура, безгранична и поэтому нельзя ограничиваться построениями только в пределах площади этого треугольника, так как в общем случае проекции плоскости занимают всю каждую из плоскостей проекций: горизонтальную П I , фронтальную П 2 и профильную П 3 .

Более наглядно плоскость может быть задана при помощи прямых, по которым она пересекает плоскости проекций (рис. 24, а).

Эти прямые называются следами плоскости. В общем случае оба следа должны пересекаться между собой в точке на оси проекций, которую называют «точкой схода следов».

Из всего многообразия положений плоскости относительно заданной системы плоскостей проекций обычно выделяют такие, когда.

Положение плоскости в пространстве может быть определено на чертеже одним из следующих способов:

1. Тремя точками, не лежащими на одной прямой (рис. 35 ).

2. Прямой и точкой, не лежащей на этой прямой (рис. 36 ).

3. Двумя пересекающимися прямыми (рис. 37) .

4. Двумя параллельными прямыми (рис. 38 ).

5. Плоской фигурой (рис. 39 ).

6. Следами (рис. 40, 41 ).

7. Параметрами плоскости.

Следы плоскости

Следом плоскости называется линия пересечения плоскости с плоскостью проекций. След плоскости обозначается той же буквой, что и плоскость с подстрочным знаком, соответствующим имени плоскости проекций, с которой пересекается данная. Если плоскость (назовем ее P ) не параллельна, какой-либо плоскости проекций, то она пересекает все три плоскости проекций и, следовательно, имеет три следа – горизонтальный P H , фронтальный P V и профильный P W (рис. 40, 41 ). Как и любая прямая, любой след плоскости имеет три проекции, но, для облегчения чтения эпюра, принято обозначать только ту проекцию следа, которая не совпадает с осью проекций. Положение любого следа плоскости, как и любой прямой, определяется положением двух ее точек. Для следов плоскости такими точками могут являться точки, называемые точками схода следов , то есть точки, в которых плоскость пересекает оси координат – P x , P y , P z . Численные значения координат x , y , и z точек схода следов называются параметрами плоскости .

Положение плоскости в пространстве может быть однозначно определено одним из хорошо известных в геометрии элементов. В соответствии с этим плоскость может быть задана одним из шести способов:

а) тремя точками, не лежащими на одной прямой;

б) прямой и точкой, не лежащей на этой прямой;

в) двумя параллельными прямыми;

г) двумя пересекающимися прямыми;

д) плоской фигурой;

е) следами.

Тогда на чертеже (рис. 3.1) соответствующие геометрические объекты (точки, прямые) выглядят в виде проекций.

Рис. 3.1. Безосный двухкартинный комплексный чертеж геометрических объектов, задающих плоскость.

3.2. Плоскости частного и общего положения

3.2.1. Плоскости уровня

Плоскостью уровня называется плоскость, параллельная одной из плоскостей проекций, а следовательно, перпендикулярная двум другим. Тогда проекциями плоскости уровня будут прямые, параллельные соответствующим осям (рис. 3.2), вне зависимости от того, чем задана плоскость. От способа задания плоскости зависит лишь ее проекция на ту плоскость проекций, которой заданная плоскость параллельна.

Плоскость, параллельная П 1 , называется горизонтальной плоскостью уровня (Г ). На рис. 3.2а она задана тремя точками.

Плоскость, параллельная П 2 , называется фронтальной плоскостью уровня (Ф ). Зададим ее параллельными прямыми (рис. 3.2б).

Плоскость, параллельная П 3 , называется профильной плоскостью уровня (Р ). Считаем ее заданной пересекающимися прямыми (рис. 3.2в).

Рис. 3.2. Плоскости уровня на комплексном чертеже.

3.2.2. Проецирующие плоскости

Проецирующей называется плоскость, перпендикулярная одной из плоскостей проекций. Исходя из определения, такая плоскость вырождается в прямую при проецировании на ту плоскость проекций, к которой она перпендикулярна.

Рис. 3.3. Проецирующие плоскости на комплексном чертеже.

Горизонтально-проецирующей называется плоскость, перпендикулярная П 1 , фронтально-проецирующей – перпендикулярная П 2 , и профильно-проецирующей – плоскость, перпендикулярная П 3 . На чертеже, первая из них задана плоской фигурой (рис. 3.3а), вторая – точкой и прямой (рис. 3.3б), третья - двумя параллельными прямыми (рис. 3.3в).

3.2.3.Плоскости общего положения

Плоскостью общего положения называется плоскость, не перпендикулярная и не параллельная ни одной из плоскостей проекций, а значит, расположенная под произвольным углом к каждой из них.

У такой плоскости все проекции будут плоские фигуры (рис. 3.4).

Рис. 3.4. Плоскость общего положения, заданная треугольником

3.3. Принадлежность точки и прямой плоскости

Точка принадлежит плоскости, если она принадлежит прямой, лежащей в этой плоскости. Принадлежность прямой плоскости определяется по одному из двух признаков:

а) прямая проходит через две точки, лежащие в этой плоскости;

б) прямая проходит через точку и параллельна прямой, лежащим в этой плоскости.

3.4. Главные линии плоскости

Главными линиями плоскости называются линии уровня, лежащие в данной плоскости. Рассмотрим построение главных линий плоскости, заданной треугольником (рис. 3.5).

Горизонталь плоскости DАВС начинаем с вычерчивания ее фронтальной проекции h 2 , которая, как известно, параллельна оси ОХ . Поскольку эта горизонталь принадлежит данной плоскости, то она проходит через две точки плоскости DАВС , а именно, точки А и 1. Имея их фронтальные проекции А 2 и 1 2 , по линии связи получим горизонтальные проекции 1 1 . Соединив точки А 1 и 1 1 , имеем горизонтальную проекцию h 1 горизонтали плоскости DАВС . Профильная проекция h 3 горизонтали плоскости DАВС будет параллельна оси ОХ по определению.

Фронталь плоскости DАВС строится аналогично (рис. 3.5) с той лишь разницей, что ее вычерчивание начинается с горизонтальной проекции f 1 , так как известно, что она параллельна оси ОХ. Профильная проекция f 3 фронтали должна быть параллельна оси ОZ .

Профильная линия плоскости DАВС имеет горизонтальную р 1 и фронтальную р 2 проекции, параллельные осям OY и OZ , а профильную проекцию р 3 можно получить по фронтальной, используя точки пересечения В и 3 с D АВС .

При построении главных линий плоскости необходимо помнить лишь одно правило: для решения задачи всегда нужно получить две точки пересечения с данной плоскостью.

Рис. 3.5. Построение главных линий плоскости, заданной треугольником

3.5. Взаимное положение прямых и плоскостей

3.5.1. Параллельность прямых и плоскостей

а). Если прямые параллельны друг другу, тогда параллельны и их одноименные проекции. б). Прямая параллельна плоскости, если она параллельна какой - либо прямой, лежащей в этой плоскости

Рис. 3.6. Построение параллельно расположенных геометрических объектов.

Тогда для построения параллельной прямой а (рис. 3.6а) необходимо, чтобы обе ее проекции были параллельны одноименным проекциям прямой (например, АВ ), лежащей в данной плоскости. в) Плоскости параллельны друг другу, если две пересекающиеся прямые одной плоскости попарно параллельны двум пересекающимся прямым другой плоскости. Для интерпретации этого свойства достаточно дополнить построения на рис. 3.6а еще одной прямой в, пересекающей а и параллельной ВС (рис. 3.6б).

3.5.2. Перпендикулярность прямых и плоскостей

а). Прямая перпендикулярна к плоскости, если она перпендикулярна к двум пересекающимся прямым, лежащим в этой плоскости, одна из которых фронталь, а другая горизонталь.

Хотя для перпендикулярности вполне достаточно, чтобы указанными пересекающимися прямыми были любые прямые в данной плоскости, однако только горизонталь и фронталь позволяют получить без искажений проекции прямого угла, образованного перпендикуляром к плоскости и фронталью (на П 2) и перпендикуляром к плоскости и горизонталью (на П 1). Тогда очевидно, что горизонтальная проекция этого перпендикуляра расположена под прямым углом к горизонтальной проекции горизонтали, а фронтальная проекция - под прямым углом к фронтальной проекции фронтали.

Рис. 3.7. Построение перпендикулярно расположенных геометрических объектов.

б). Плоскости перпендикулярны друг к другу, если одна из них содержит перпендикуляр к другой.

Обратимся к рис. 3.7а, где перпендикуляр g к плоскости уже построен, необходимо через точку D провести произвольную прямую q (рис. 3.7б).

3.6. Позиционные задачи на плоскости

Позиционными называются задачи на определение каких-либо общих элементов геометрических объектов, например, точки пересечения прямой и плоскости, линии пересечения двух плоскостей.

3.6.1. Пересечение прямой и плоскости

Задачу на пересечение прямой и плоскости можно решать с помощью вспомогательной секущей плоскости, которая должна удовлетворять следующим условиям:

а) быть плоскостью частного положения, так как именно плоскость частного положения проецируется на соответствующую плоскость проекций в виде прямой;

б) проходить через прямую, точку пересечения которой с плоскостью мы отыскиваем.

Рассмотрим сначала частный случай. Пусть плоскость занимает частное положение в пространстве, например, является горизонтально - проецирующей и задана треугольником АВС (рис. 3.8 а). Необходимо найти точку пересечения ее с прямой а , заданной произвольно. Поскольку на П 1 горизонтально–проецирующая плоскость вырождается в прямую S 1 , то горизонтальной проекцией точки пересечения будет К 1 . Далее по линии связи на прямой а 2 (очевидно точка пересечения К принадлежит прямой а) найдем фронтальную проекцию К 2 точки пересечения.

Осталось определить видимые участки прямой а , поскольку на П 2 часть указанной прямой будет закрыта от наблюдателя плоскостью DАВС . Для этого необходимо рассмотреть точку, где пересекаются фронтальные проекции а и какой-либо прямой (например, АС ), лежащей в плоскости DАВС . Обозначим эту точку 1 2 . Но пересекаться прямая а и DАВС могут только в одной точке, которую мы отыскали (К 2). Все остальные точки будут точками, где они скрещиваются. Следовательно, прямая а и АС скрещиваются в пространстве. Значит, все точки, где пересекаются их проекции, будут конкурирующими, а именно 1 2 =2 2 . Тогда на П 1 имеем по линии связи 1 1 ÎА 1 С 1 и 2 1 Î а 1 . Видимой является точка 2, которая принадлежит прямой а . Это сохраняется до точки пересечения К 2 . Затем, естественно, участок прямой а будет невидим (обозначается пунктирной линией) до выхода из-под плоскости DАВС . Теперь задачу можно считать полностью решенной.

Рассмотрим общий случай пересечения прямой и плоскости, когда обе они занимают общее положение в пространстве. Пусть плоскость задана треугольником DАВС . Здесь и в дальнейшем используем задание плоскости в основном треугольником, так как в этом случае решение задачи наиболее наглядно. Необходимо найти точку пересечения произвольно заданной прямой в с DАВС (рис. 3.8, б).

Как указано выше, нужно через прямую в провести плоскость частного положения (например, фронтально-проецирующую). Линия пересечения этой плоскости совпадает с прямой в на П 2, т.е. S 2 =в 2 . Тогда по точкам пересечения 3 2 и 4 2 построим точки 3 1 и 4 1 , а следовательно, и прямую 3 1 4 1 , являющуюся горизонтальной проекцией линии пересечения плоскости S и DАВС . Но так как прямая 34ÌDАВС, то точка К 1 будет горизонтальной проекцией точки пересечения прямой в и DАВС. По ней найдем и фронтальную проекцию К 2 , которая, очевидно, должна быть расположена на в 2 (ведь точка пересечения принадлежит и прямой в и D АВС).

Рис. 3.8. Пересечение прямой и плоскости

Определим видимые участки прямой в на обеих проекциях по конкурирующим точкам. Для определения видимости на П 2 используем фронтально-конкурирующие точки (например, точки 3 2 =5 2 , где скрещиваются в 2 и А 2 В 2). Очевидно, что точка 3 1 ближе к нам, чем точка 5 1 . Следовательно, на П 2 выше 3 2 , тогда в этой точке А 2 В 2 выше, а в 2 лежит под ней. Это верно только до точки пересечения К 2 . Далее, естественно, выше будет в 2 . Аналогично по горизонтально–конкурирующим точкам (например, 6 1 =7 1) определяем, что в точках 6 1 =7 1 прямая В 1 С 1 лежит выше, чем в 1 , так как точка 7 2 расположена выше, чем точка 6 2 . Невидимый участок прямой в обозначаем пунктирной линией.

3.6.2. Пересечение плоскостей. Метод вспомогательных секущих плоскостей

Поскольку линией пересечения двух плоскостей является прямая, то для ее построения необходимо определить лишь две точки пересечения плоскостей.

Для решения указанной задачи применяется метод вспомогательных секущих плоскостей, который заключается в следующем.

Вводятся две дополнительные плоскости, пересекающие заданные. Для каждой дополнительной (вспомогательной) плоскости строим линию ее пересечения с заданными плоскостями. Точка пересечения двух полученных линий и будет точкой пересечения заданных плоскостей. Поскольку дополнительных плоскостей две, то и точек пересечения заданных плоскостей тоже две. Соединяя их, получаем линию пересечения плоскостей. Разумеется, каждая дополнительная плоскость должна занимать частное положение в пространстве, тогда на плоскость проекций, к которой вспомогательная плоскость перпендикулярна, она проецируется в прямую. Иначе, если вспомогательная плоскость занимает общее положение, введение дополнительной плоскости не упрощает решение задачи.

Проиллюстрируем на двух примерах.

Найти линию пересечения двух треугольников АВС и DEF и определить видимость сторон (рис. 3.9). Построим линию пересечения треугольников, воспользовавшись методом дополнительных секущих плоскостей. Для упрощения решения задачи секущие плоскости будем проводить через стороны треугольников.

Рис. 3.9. Пересечение двух треугольников

Пусть дополнительная горизонтально–проецирующая плоскость S проходит через сторону DE . Тогда S 1 = D 1 E 1 . Это и есть горизонтальная проекция линии пересечения S с DАВС и DDEF . Построим фронтальную проекцию. Для DDEF таковой является, очевидно, D 2 E 2 . Для DАВС по горизонтальным проекциям 1 1 и 2 1 точек пересечения найдем их фронтальные проекции 1 2 и 2 2 , соединив которые, получим фронтальную проекцию линии пересечения плоскости S и DАВС . Продлив линии D 2 E 2 и 1 2 2 2 , найдем точку их пересечения N 2 *, которая и является точкой пересечения плоскостей, заданных треугольниками. Надо заметить, что точка N 2 * не принадлежит треугольникам, поэтому и является точкой пересечения не треугольников, а плоскостей, в которых лежат треугольники.

Аналогично, вводя дополнительную горизонтально–проецирующую плоскость S*, проходящую через сторону ВС треугольника АВС , найдем точку М 2 пересечения заданных треугольников.

Соединив точки N 2 * и M 2 , найдем фронтальную проекцию линии пересечения плоскостей треугольников АВС и DEF. Выделив участок N 2 M 2 , лежащий в плоскости обоих треугольников, получаем фронтальную проекцию линии пересечения треугольников АВС и DEF. По токам N 2 M 2 , определяем и горизонтальную проекцию N 1 M 1 линии пересечения заданных треугольников. Следует заметить, что дополнительные плоскости выбраны нами совершенно произвольно. Видимость сторон, а вместе с ними и отдельных частей треугольников определяется с помощью конкурирующих точек. Две такие точки уже имеются (2 1 =3 1). Из рассмотрения фронтальных проекций, очевидно, что 2 1 невидимая. Значит, в этой точке прямая D 1 E 1 выше В 1 С 1 , а следовательно, она выше по всей длине, так как плоскость треугольника DА 1 В 1 С 1 нигде не пересекает. Тогда с другой стороны от N 1 M 1 плоскость треугольника D 1 E 1 F 1 будет ниже. Аналогично определяем видимость на фронтальной проекции, рассматривая кокурирующие точки 5 и 6 на скрещивающихся прямых DE и АВ (рис. 3.9). В случае затруднений в определении видимости можно использовать несколько пар скрещивающихся сторон заданных треугольников.

Положение плоскости в пространстве определяется:

тремя точками, не лежащими на одной прямой;
прямой и точкой, взятой вне прямой;
двумя пересекающимися прямыми;
двумя параллельными прямыми;
плоской фигурой.

В соответствии с этим на эпюре плоскость может быть задана:

проекциями трёх точек, не лежащих на одной прямой (Рисунок 3.1,а);
проекциями точки и прямой (Рисунок 3.1,б);
проекциями двух пересекающихся прямых (Рисунок 3.1,в);
проекциями двух параллельных прямых (Рисунок 3.1,г);
плоской фигурой (Рисунок 3.1,д);
следами плоскости;
линией наибольшего ската плоскости.

Рисунок 3.1 – Способы задания плоскостей

Плоскость общего положения – это плоскость, которая не параллельна и не перпендикулярна ни одной из плоскостей проекций.

Следом плоскости называется прямая, полученная в результате пересечения заданной плоскости с одной из плоскостей проекций.

Плоскость общего положения может иметь три следа: горизонтальный – απ 1 , фронтальный – απ 2 и профильный – απ 3 , которые она образует при пересечении с известными плоскостями проекций: горизонтальной π 1 , фронтальной π 2 и профильной π 3 (Рисунок 3.2).

Рисунок 3.2 – Следы плоскости общего положения

3.2. Плоскости частного положения

Плоскость частного положения – плоскость, перпендикулярная или параллельная плоскости проекций.

Плоскость, перпендикулярная плоскости проекций, называется проецирующей и на эту плоскость проекций она будет проецироваться в виде прямой линии.

Свойство проецирующей плоскости : все точки, линии, плоские фигуры, принадлежащие проецирующей плоскости, имеют проекции на наклонном следе плоскости (Рисунок 3.3).

Рисунок 3.3 – Фронтально-проецирующая плоскость, которой принадлежат: точки А , В , С ; линии АС , АВ , ВС ; плоскость треугольника АВС

Фронтально-проецирующая плоскость – плоскость, перпендикулярная фронтальной плоскости проекций (Рисунок 3.4, а).

Горизонтально-проецирующая плоскость – плоскость, перпендикулярная горизонтальной плоскости проекций (Рисунок 3.4, б).

Профильно-проецирующая плоскость – плоскость, перпендикулярная профильной плоскости проекций .

Плоскости, параллельные плоскостям проекций, называются плоскостями уровня или дважды проецирующими плоскостями .

Фронтальная плоскость уровня – плоскость, параллельная фронтальной плоскости проекций (Рисунок 3.4, в).

Горизонтальная плоскость уровня – плоскость, параллельная горизонтальной плоскости проекций (Рисунок 3.4, г).

Профильная плоскость уровня – плоскость, параллельная профильной плоскости проекций (Рисунок 3.4, д).

Рисунок 3.4 – Эпюры плоскостей частного положения

3.3. Точка и прямая в плоскости. Принадлежность точки и прямой плоскости

Точка принадлежит плоскости, если она принадлежит какой-либо прямой, лежащей в этой плоскости (Рисунок 3.5).

Прямая принадлежит плоскости, если она имеет с плоскостью хотя бы две общие точки (Рисунок 3.6).

Рисунок 3.5 – Принадлежность точки плоскости

α = m // n

D ∈ n ⇒ D ∈ α

Рисунок 3.6 – Принадлежность прямой плоскости

Упражнение

Дана плоскость, заданная четырехугольником (Рисунок 3.7, а). Необходимо достроить горизонтальную проекцию вершины С .


а	б

Рисунок 3.7 – Решение задачи

Решение :

ABCD – плоский четырехугольник, задающий плоскость.
Проведём в нём диагонали AC и BD (Рисунок 3.7, б), которые являются пересекающимися прямыми, также задающими ту же плоскость.
Согласно признаку пересекающихся прямых, построим горизонтальную проекцию точки пересечения этих прямых — K по её известной фронтальной проекции: A 2 C 2 ∩ B 2 D 2 =K 2 .
Восстановим линию проекционной связи до пересечения с горизонтальной проекцией прямой BD : на проекции диагонали B 1 D 1 строим К 1 .
Через А 1 К 1 проводим проекцию диагонали А 1 С 1 .
Точку С 1 получаем, посредством линии проекционной связи до пересечения её с горизонтальной проекцией продолженной диагонали А 1 К 1 .

3.4. Главные линии плоскости

В плоскости можно построить бесконечное множество прямых, но есть особые прямые, лежащие в плоскости, называемые главными линиями плоскости (Рисунок 3.8 – 3.11).

Прямой уровня или параллелью плоскости называется прямая, лежащая в данной плоскости и параллельная одной из плоскостей проекций.

Горизонталь или горизонтальная прямая уровня h (первая параллель) – это прямая, лежащая в данной плоскости и параллельная горизонтальной плоскости проекций (π 1) (Рисунок 3.8, а; 3.9).

Фронталь или фронтальная прямая уровня f (вторая параллель) – это прямая лежащая в данной плоскости и параллельная фронтальной плоскости проекций (π 2) (Рисунок 3.8, б; 3.10).

Профильная прямая уровня p (третья параллель) – это прямая лежащая в данной плоскости и параллельная профильной плоскости проекций (π 3) (Рисунок 3.8, в; 3.11).

Рисунок 3.8 а – Горизонтальная прямая уровня в плоскости, заданной треугольником

Рисунок 3.8 б – Фронтальная прямая уровня в плоскости, заданной треугольником

Рисунок 3.8 в – Профильная прямая уровня в плоскости, заданной треугольником

Рисунок 3.9 – Горизонтальная прямая уровня в плоскости, заданной следами

Рисунок 3.10 – Фронтальная прямая уровня в плоскости, заданной следами

Рисунок 3.11 – Профильная прямая уровня в плоскости, заданной следами

3.5. Взаимное положение прямой и плоскости

Прямая по отношению к заданной плоскости может быть параллельной и может с ней иметь общую точку, то есть пересекаться.

3.5.1. Параллельность прямой плоскости

Признак параллельности прямой плоскости : прямая параллельна плоскости, если она параллельна какой-либо прямой, принадлежащей этой плоскости (Рисунок 3.12).

Рисунок 3.12 – Параллельность прямой плоскости

3.5.2. Пересечение прямой с плоскостью

Для построения точки пересечения прямой с плоскостью общего положения (Рисунок 3.13), необходимо:

Заключить прямую а во вспомогательную плоскость β (в качестве вспомогательной плоскости следует выбирать плоскости частного положения);
Найти линию пересечения вспомогательной плоскости β с заданной плоскостью α;
Найти точку пересечения заданной прямой а с линией пересечения плоскостей MN .

Рисунок 3.13 – Построение точки встречи прямой с плоскостью

Упражнение

Заданы: прямая АВ общего положения, плоскость σ⊥π 1 . (Рисунок 3.14). Построить точку пересечения прямой АВ с плоскостью σ.

Решение :

Плоскость σ – горизонтально-проецирующая, следовательно, горизонтальной проекцией плоскости σ является прямая σ 1 (горизонтальный след плоскости);
Точка К должна принадлежать прямой АВ ⇒ К 1 ∈А 1 В 1 и заданной плоскости σ ⇒ К 1 ∈σ 1 , следовательно, К 1 находится в точке пересечения проекций А 1 В 1 и σ 1 ;
Фронтальную проекцию точки К находим посредством линии проекционной связи: К 2 ∈А 2 В 2 .

Рисунок 3.14 – Пересечение прямой общего положения с плоскостью частного положения

Упражнение

Заданы: плоскость σ = ΔАВС – общего положения, прямая EF (Рисунок 3.15).

Требуется построить точку пересечения прямой EF с плоскостью σ.


а	б

Рисунок 3.15 – Пересечение прямой с плоскостью

Заключим прямую EF во вспомогательную плоскость, в качестве которой воспользуемся горизонтально-проецирующей плоскостью α (Рисунок 3.15, а);
Если α⊥π 1 , то на плоскость проекций π 1 плоскость α проецируется в прямую (горизонтальный след плоскости απ 1 или α 1), совпадающую с E 1 F 1 ;
Найдём прямую пересечения (1-2) проецирующей плоскости α с плоскостью σ (решение подобной задачи будет рассмотрено );
Прямая (1-2) и заданная прямая EF лежат в одной плоскости α и пересекаются в точке K .

Алгоритм решения задачи (Рисунок 3.15, б):

Через EF проведем вспомогательную плоскость α:

3.6. Определение видимости методом конкурирующих точек

При оценке положения данной прямой, необходимо определить – точка какого участка прямой расположена ближе (дальше) к нам, как к наблюдателям, при взгляде на плоскость проекций π 1 или π 2 .

Точки, которые принадлежат разным объектам, а на одной из плоскостей проекций их проекции совпадают (то есть, две точки проецируются в одну), называются конкурирующими на этой плоскости проекций .

Необходимо отдельно определить видимость на каждой плоскости проекций.

Видимость на π 2 (рис. 3.15)

Выберем точки, конкурирующие на π 2 – точки 3 и 4. Пусть точка 3∈ВС∈σ , точка 4∈EF .

Чтобы определить видимость точек на плоскости проекций π 2 надо определить расположение этих точек на горизонтальной плоскости проекций при взгляде на π 2 .

Направление взгляда на π 2 показано стрелкой.

По горизонтальным проекциям точек 3 и 4, при взгляде на π 2 , видно, что точка 4 1 располагается ближе к наблюдателю, чем 3 1 .

4 1 ∈E 1 F 1 ⇒ 4∈EF ⇒ на π 2 будет видима точка 4, лежащая на прямой EF , следовательно, прямая EF на участке рассматриваемых конкурирующих точек расположена перед плоскостью σ и будет видима до точки K

Видимость на π 1

Для определения видимости выберем точки, конкурирующие на π 1 – точки 2 и 5.

Чтобы определить видимость точек на плоскости проекций π 1 надо определить расположение этих точек на фронтальной плоскости проекций при взгляде на π 1 .

Направление взгляда на π 1 показано стрелкой.

По фронтальным проекциям точек 2 и 5, при взгляде на π 1 , видно, что точка 2 2 располагается ближе к наблюдателю, чем 5 2 .

2 1 ∈А 2 В 2 ⇒ 2∈АВ ⇒ на π 1 будет видима точка 2, лежащая на прямой АВ , следовательно, прямая EF на участке рассматриваемых конкурирующих точек расположена под плоскостью σ и будет невидима до точки K – точки пересечения прямой с плоскостью σ.

Видимой из двух конкурирующих точек будет та, у которой координата «Z» или(и) «Y» больше.

3.7. Перпендикулярность прямой плоскости

Признак перпендикулярности прямой плоскости : прямая перпендикулярна плоскости, если она перпендикулярна двум пересекающимся прямым, лежащим в данной плоскости.


а	б

Рисунок 3.16 – Задание прямой, перпендикулярной плоскости

Теорема. Если прямая перпендикулярна плоскости, то на эпюре: горизонтальная проекции прямой перпендикулярна горизонтальной проекции горизонтали плоскости, а фронтальная проекция прямой перпендикулярна фронтальной проекции фронтали (Рисунок 3.16, б)

Теорема доказывается через теорему о проецировании прямого угла в частном случае.

Если плоскость задана следами, то проекции прямой перпендикулярной плоскости перпендикулярны соответствующим следам плоскости (Рисунок 3.16, а).

Пусть прямая p перпендикулярна плоскости σ=ΔАВС и проходит через точку K .

Построим горизонталь и фронталь в плоскости σ=ΔАВС : A-1 ∈σ; A-1 //π 1 ; С-2 ∈σ; С-2 //π 2 .
Восстановим из точки K перпендикуляр к заданной плоскости: p 1 ⊥h 1 и p 2 ⊥f 2 , или p 1 ⊥απ 1 и p 2 ⊥απ 2

3.8. Взаимное положение двух плоскостей

3.8.1. Параллельность плоскостей

Две плоскости могут быть параллельными и пересекающимися между собой.

Признак параллельности двух плоскостей : две плоскости взаимно параллельны, если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости.

Упражнение

Задана плоскость общего положения α=ΔАВС и точка F ∉α (Рисунок 3.17).

Через точку F провести плоскость β, параллельную плоскости α.

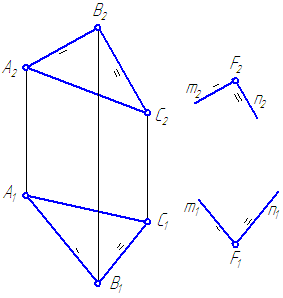
Рисунок 3.17 – Построение плоскости, параллельной заданной

Решение :

В качестве пересекающихся прямых плоскости α возьмем, например, стороны треугольника АВ и ВС.

Через точку F проводим прямую m , параллельную, например, АВ .
Через точку F , или же через любую точку, принадлежащую m , проводим прямую n , параллельную, например, ВС , причём m∩ n=F .
β = m ∩n и β//α по определению.

3.8.2. Пересечение плоскостей

Результатом пересечения 2-х плоскостей является прямая. Любая прямая на плоскости или в пространстве может быть однозначно задана двумя точками. Поэтому для того, чтобы построить линию пересечения двух плоскостей, следует найти две точки, общие для обеих плоскостей, после чего соединить их.

Рассмотрим примеры пересечения двух плоскостей при различных способах их задания: следами; тремя точками, не лежащими на одной прямой; параллельными прямыми; пересекающимися прямыми и др.

Упражнение

Две плоскости α и β заданы следами (Рисунок 3.18). Построить линию пересечения плоскостей.

Рисунок 3.18 – Пересечение плоскостей общего положения, заданных следами

Порядок построения линии пересечения плоскостей :

Найти точку пересечения горизонтальных следов — это точка М (её проекции М 1 и М 2 , при этом М 1 =М , т.к. М – точка частного положения, принадлежащая плоскости π 1).
Найти точку пересечения фронтальных следов — это точка N (её проекции N 1 и N 2 , при этом N 2 = N , т.к. N – точка частного положения, принадлежащая плоскости π 2).
Построить линию пересечения плоскостей, соединив одноименные проекции полученных точек: М 1 N 1 и М 2 N 2 .

М N – линия пересечения плоскостей.

Упражнение

Задана плоскость σ = ΔАВС , плоскость α – горизонтально- проецирующая (α⊥π 1) ⇒α 1 – горизонтальный след плоскости (Рисунок 3.19).

Построить линию пересечения этих плоскостей.

Решение :

Так как плоскость α пересекает стороны АВ и АС треугольника АВС , то точки пересечения K и L этих сторон с плоскостью α являются общими для обеих заданных плоскостей, что позволит, соединив их, найти искомую линию пересечения.

Точки могут быть найдены как точки пересечения прямых с проецирующей плоскостью: находим горизонтальные проекции точек K и L , то есть K 1 и L 1 , на пересечении горизонтального следа (α 1) заданной плоскости α с горизонтальными проекциями сторон ΔАВС : А 1 В 1 и A 1 C 1 . После чего посредством линий проекционной связи находим фронтальные проекции этих точек K 2 и L 2 на фронтальных проекциях прямых АВ и АС . Соединим одноимённые проекции: K 1 и L 1 ; K 2 и L 2 . Линия пересечения заданных плоскостей построена.

Алгоритм решения задачи :

KL – линия пересечения ΔАВС и σ (α∩σ = KL ).

Рисунок 3.19 – Пересечение плоскостей общего и частного положения

Упражнение

Заданы плоскости α = m//n и плоскость β = ΔАВС (Рисунок 3.20).

Построить линию пересечения заданных плоскостей.

Решение :

Чтобы найти точки, общие для обеих заданных плоскостей и задающие линию пересечения плоскостей α и β, необходимо воспользоваться вспомогательными плоскостями частного положения.
В качестве таких плоскостей выберем две вспомогательные плоскости частного положения, например: σ // τ; σ⊥π 2 ; τ⊥π 2 .
Вновь введённые плоскости пересекаются с каждой из заданных плоскостей α и β по прямым, параллельным друг другу, так как σ // τ:

— результатом пересечения плоскостей α, σ и τ являются прямые (4-5) и (6-7);

— результатом пересечения плоскостей β, σ и τ являются прямые (3-2) и (1-8).

Прямые (4-5) и (3-2) лежат в плоскости σ; точка их пересечения М одновременно лежит в плоскостях α и β, то есть на прямой пересечения этих плоскостей;
Аналогично находим точку N , общую для плоскостей α и β.
Соединив точки M и N , построим прямую пересечения плоскостей α и β.

Рисунок 3.20 – Пересечение двух плоскостей общего положения (общий случай)

Алгоритм решения задачи :

Упражнение

Заданы плоскости α = ΔАВС и β = a //b . Построить линию пересечения заданных плоскостей (Рисунок 3.21).

Рисунок 3.21 Решение задачи на пересечение плоскостей

Решение :

Воспользуемся вспомогательными секущими плоскостями частного положения. Введём их так, чтобы сократить количество построений. Например, введём плоскость σ⊥π 2 , заключив прямую a во вспомогательную плоскость σ (σ∈a ). Плоскость σ пересекает плоскость α по прямой (1-2), а σ∩β=а . Следовательно (1-2)∩а =K .

Точка К принадлежит обеим плоскостям α и β.

Следовательно, точка K , является одной из искомых точек, через которые проходит прямая пересечения заданных плоскостей α и β.

Для нахождения второй точки, принадлежащей прямой пересечения α и β, заключим прямую b во вспомогательную плоскость τ⊥π 2 (τ∈b ).

Соединив точки K и L , получим прямую пересечения плоскостей α и β.

3.8.3. Взаимно перпендикулярные плоскости

Плоскости взаимно перпендикулярны, если одна из них проходит через перпендикуляр к другой.

Упражнение

Задана плоскость σ⊥π 2 и прямая общего положения – DE (Рисунок 3.22)

Требуется построить через DE плоскость τ⊥σ.

Решение .

Проведём перпендикуляр CD к плоскости σ – C 2 D 2 ⊥σ 2 (на основании ).

Рисунок 3.22 – Построение плоскости, перпендикулярной к заданной плоскости

По теореме о проецировании прямого угла C 1 D 1 должна быть параллельна оси проекций. Пересекающиеся прямые CD∩ DE задают плоскость τ. Итак, τ⊥σ.

Аналогичные рассуждения, в случае плоскости общего положения.

Упражнение

Задана плоскость α = ΔАВС и точка K вне плоскости α.

Требуется построить плоскость β⊥α, проходящую через точку K .

Алгоритм решения (Рисунок 3.23):

Построим горизонталь h и фронталь f в заданной плоскости α = ΔАВС ;
Через точку K проведём перпендикуляр b к плоскости α (по теореме о перпендикуляре к плоскости : если прямая перпендикулярна плоскости, то её проекции перпендикулярны к наклонным проекциям горизонтали и фронтали, лежащих в плоскости: b 2 ⊥f 2 ; b 1 ⊥h 1 ;
Задаём плоскость β любым способом, например, β = a∩ b , таким образом, плоскость, перпендикулярная к заданной, построена: α⊥β.